这道题看起来是用搜索算法，实则是一个数论大题。

首先根据题意，我们可以先写一个暴力搜索代码（DFS）：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll inf=2e9,f[10]={6,2,5,5,4,5,6,3,7,6};
ll i,ans;
void dfs(ll gz,ll x){
	if(gz>i)return;
	if(gz==i)return ans=min(ans,x),void();
	for(ll i=0;i<=9;i++){
		if(i==0&&gz==0)continue;
		dfs(gz+f[i],x*10+i);
	}
}
int main(){
	for(i=1;i<=40;i++){
		ans=inf;
		dfs(0,0);
		cout<<i<<"的答案是"<<ans<<'\n';
	}
}

然后我们可以得出 1≤n≤40 时的答案如下。（搜到 40就炸了）

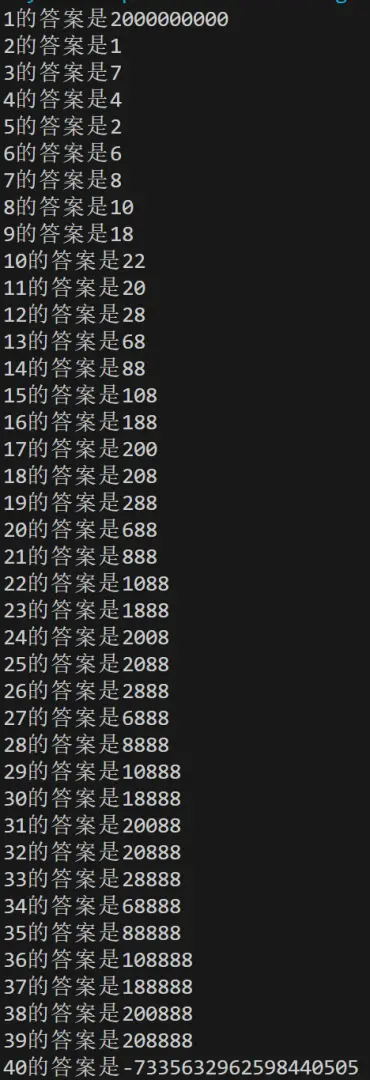
于是我们可以发现DFS的代码只可以得到30分。 但是观察发现好像又有规律。 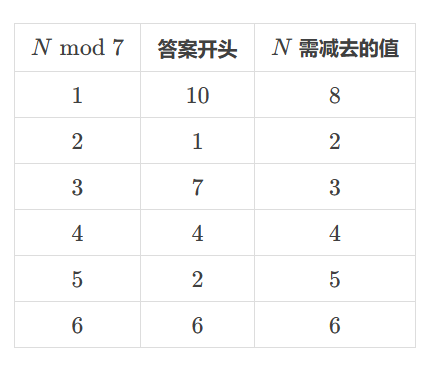N mod 7，可以得到答案的开头，然后剩下就是8，有多少个8。 最后我们再处理一些特例，（比如：1，10等等）

#include<bits/stdc++.h>
using namespace std;
const int f[10]={0,-1,1,7,4,2,6,8,10};
int T,n,d,i;
int main(){
	for(cin>>T;T--;){
		cin>>n;
		if(n<=8)cout<<f[n];
		else{
			d=n%7;
			if(!d)for(i=1;i<=n/7;i++)cout<<8;
			if(d==1){
				cout<<10;
				for(i=1;i<n/7;i++)cout<<8;
			}
			if(d==2){
				cout<<1;
				for(i=1;i<=n/7;i++)cout<<8;
			}
			if(d==3){
				if(n==10)cout<<22;
				else{
					cout<<200;
					for(i=1;i<=n/7-2;i++)cout<<8;
				}
			}
			if(d==4){
				cout<<20;
				for(i=1;i<n/7;i++)cout<<8;
			}
			if(d==5){
				cout<<2;
				for(i=1;i<=n/7;i++)cout<<8;
			}
			if(d==6){
				cout<<6;
				for(i=1;i<=n/7;i++)cout<<8;
			}
		}
		cout<<'\n';
	}
}